An ever so very slightly embroidered recounting of the problem
It is party time chez Eastaway as one of the nation’s favourite mathematicians Rob and his wife have invited six people round for dinner. The desserts have been cleared and as the quests settle back with coffee and liqueurs, they turn to each other and embark on long conversations with the person to their left or right.
 Lulled by the flickering candlelight, Rob idly muses that he has three possible outcomes: chat to the redhead on his right, be talked at by the stern brunette to his left or have no one to converse with all and end up a ‘gooseberry’ in the middle.
Lulled by the flickering candlelight, Rob idly muses that he has three possible outcomes: chat to the redhead on his right, be talked at by the stern brunette to his left or have no one to converse with all and end up a ‘gooseberry’ in the middle.
The next day, Rob receives an email from Mr H, the nice maths teacher, asking if there is anything he can tackle while on a health-related sabbatical. Deciding that Mr H owes him a favour, he sets him to work on the problem.
Solving the Problem
I started by trying a few ideas in Excel and soon realised that 8 people was going to be a very complex task! I then used a key mathematical technique which was to reduce the problem to a simpler version, solve that, then extend that solution to the larger puzzle.
Two, Three and Four People

These simplest versions are trivial so I shall leave them for you the reader to deduce.
Five People [Yes, a pentagonal-ish Lego table; I was pleased!]
 This is the first version where the problem gets interesting and where I soon hit an issue with the base logic I was using. Since there are five people and each person can turn left or right there are 25 or 32 possible permutations with everyone having turned once. I used decimal to binary to create the five digit values; with 0 for left and 1 for right; note that the binary term is calculated on one less than the permutation number. The orientations of the dinner guests are then created by selecting the digits in order using the MID string function and setting left for zero and right for one. Here are the first eight rows:
This is the first version where the problem gets interesting and where I soon hit an issue with the base logic I was using. Since there are five people and each person can turn left or right there are 25 or 32 possible permutations with everyone having turned once. I used decimal to binary to create the five digit values; with 0 for left and 1 for right; note that the binary term is calculated on one less than the permutation number. The orientations of the dinner guests are then created by selecting the digits in order using the MID string function and setting left for zero and right for one. Here are the first eight rows:
| Perm | Binary | 1 | 2 | 3 | 4 | 5 |
| 1 | 00000 | L | L | L | L | L |
| 2 | 00001 | L | L | L | L | R |
| 3 | 00010 | L | L | L | R | L |
| 4 | 00011 | L | L | L | R | R |
| 5 | 00100 | L | L | R | L | L |
| 6 | 00101 | L | L | R | L | R |
| 7 | 00110 | L | L | R | R | L |
| 8 | 00111 | L | L | R | R | R |
If we consider permutation 28 then 2710 = 110112 becomes right, right, left, right, right; for the purposes of these examples I have taken the directions to be as we see them and set the people out in a line. I then tested for matching adjacent pairs so here Pilot Penn and Luscious Liz are facing each other and start conversing.
 The others then have to change direction to see if they can get into a conversing pair. However, without additional strictures in place you end up with people being like windscreen wipers going left and right in sync, never coming face to face!
The others then have to change direction to see if they can get into a conversing pair. However, without additional strictures in place you end up with people being like windscreen wipers going left and right in sync, never coming face to face! Putting the problem back into real life provided the solution to this issue. If it is obvious the pair on the left are stuck in deep conversation you would look right and stay looking right. In our example, Lady Alexander does not need to look left again so will very soon talk at Mr H, leaving Rob as the ‘gooseberry’. This solved most of the issue but there was one group of arrangements that needed further thinking.
Three in a row
 If we now take as an example permutation 8 so that we get 710 = 001112 giving left, left, right, right, right. We have to remember that persons 1 and 5 are also sat next to each other at the round table so Rob and Mr H can talk about a common interest, like the inability of English batsmen to build an innings. Pilot Penn now has a converser to the left so he will turn right. Similarly, Lady Alexander will now turn to the left. Luscious Liz now has the casting vote as to who become the ‘gooseberry’. This means in the simulation we have to introduce a random variable so that each permutation does not necessarily derive the some outcome each time. This will apply for every combination that starts with one pair and three potential ‘gooseberries’. Our original thirty-two possibilities will clearly escalate but this is still a manageable problem to account for every possible outcome, if rather time consuming even using Excel, and confirm the not unexpected probability of being a ‘gooseberry’ is a fifth or:
If we now take as an example permutation 8 so that we get 710 = 001112 giving left, left, right, right, right. We have to remember that persons 1 and 5 are also sat next to each other at the round table so Rob and Mr H can talk about a common interest, like the inability of English batsmen to build an innings. Pilot Penn now has a converser to the left so he will turn right. Similarly, Lady Alexander will now turn to the left. Luscious Liz now has the casting vote as to who become the ‘gooseberry’. This means in the simulation we have to introduce a random variable so that each permutation does not necessarily derive the some outcome each time. This will apply for every combination that starts with one pair and three potential ‘gooseberries’. Our original thirty-two possibilities will clearly escalate but this is still a manageable problem to account for every possible outcome, if rather time consuming even using Excel, and confirm the not unexpected probability of being a ‘gooseberry’ is a fifth or:
p(g5)=0.2
Evidently, [Rob will no doubt enjoy the Fronted Adverbial here!] as we increase the number of people round the table, the potential for groups of undecided guests increases. Thus with the original problem, the worst case scenario has just one conversing pair, two adjacent guests who will turn away and four in the middle who have to be set randomly. At this point the large number of possible outcomes means that a more flexible approach is needed.
The Monte Carlo Method
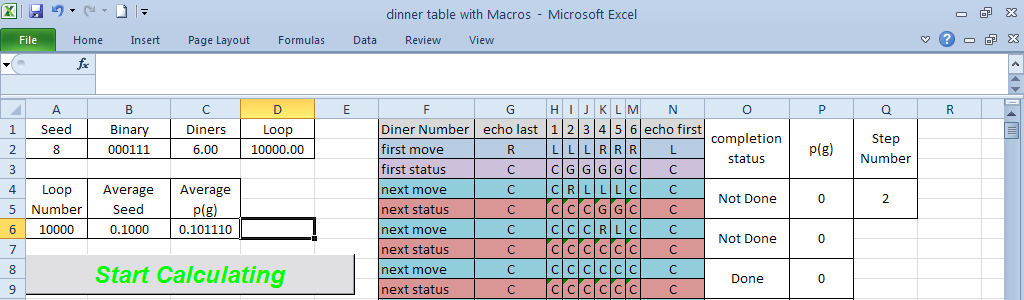
For problems when it is difficult to calculate all the possible outcomes we can compute a large number of randomised solutions and average them. The Monte Carlo method was first formalised by Stanislaw Ulam and John von Neumann when working on behaviour of sub atomic particles. Being secret work, they used a code name to describe the process, which referred to the casino in Monaco. The implementation in this instance works as follows:  I used a simple spreadsheet in Excel to test for converser or ‘gooseberry’ and a short VBA program to run the simulation. The seed for the binary code is generated randomly and the number of guests set for that worksheet. The number of loops required and a seed value for the probability are input. After testing for the initial arrangement there is a stack of move and status pairs so that however unusual the sequence of initial positions and changes, the guests will settle to a stable configuration. The step number indicates which pair that is, so that the probability for the arrangement can be stored and used for calculation.
I used a simple spreadsheet in Excel to test for converser or ‘gooseberry’ and a short VBA program to run the simulation. The seed for the binary code is generated randomly and the number of guests set for that worksheet. The number of loops required and a seed value for the probability are input. After testing for the initial arrangement there is a stack of move and status pairs so that however unusual the sequence of initial positions and changes, the guests will settle to a stable configuration. The step number indicates which pair that is, so that the probability for the arrangement can be stored and used for calculation.
Here is the VBA program which is started by pressing the large button, obviously!
Sub MonteCarlo()
‘declare the variables
Dim TheLoop As Long
Dim LoopNumber As Long
Dim ProbNumber As Double
Dim ProbAverage As Double
Dim ProbRow As Integer
Dim ProbColumn As Integer
Dim StepNumber As Integer
Dim Guests As Integer
Dim ResultsAverage() As Double
Dim ResultsNumber() As Double
‘set initial values of required loops, probability seed and number of guests
LoopNumber = Range(“D2”).Value
ProbAverage = Range(“B6”).Value
Guests = Range(“C2”).Value
‘clear storage area and set up arrays for the running average and separate probabilities
Range(“Values!A:C”) = “”
ReDim ResultsAverage(1 To LoopNumber) As Double
ReDim ResultsNumber(1 To LoopNumber) As Double
‘main program loop
For TheLoop = 1 To LoopNumber
‘display current values and generate new binary seed
Range(“A6”).Value = TheLoop
Range(“C6”).Value = ProbAverage
Calculate
‘see where all guests are in fixed position and set cell values for required p(g)
StepNumber = Cells(4, 11 + Guests).Value
ProbRow = 4 + 2 * StepNumber ‘moves down to first fixed position
ProbColumn = 10 + Guests ‘allows code to run for different numbers of guests
‘find p(g) for that arrangement and calculate new average probability
ProbNumber = Cells(ProbRow, ProbColumn).Value
ProbAverage = (ProbAverage * (TheLoop) + ProbNumber) / (TheLoop + 1)
‘store values in the storage array
ResultsNumber(TheLoop) = ProbNumber
ResultsAverage(TheLoop) = ProbAverage
‘go again!
Next TheLoop
‘fill the storage area with the results
For TheLoop = 1 To LoopNumber
Sheets(“Values”).Cells(TheLoop, “A”) = TheLoop
Sheets(“Values”).Cells(TheLoop, “B”) = ResultsNumber(TheLoop)
Sheets(“Values”).Cells(TheLoop, “C”) = ResultsAverage(TheLoop)
Next TheLoop
End Sub
The process on my old XP powered PC was rather slow due mainly to the refreshing of the guests each time. However, it did allow me to watch the change in the figures diminish over time as they approached the true value. Reducing the visible window to just the output values helped increase the speed significantly.
Six People
There are two possible outcomes: all six in conversation or two pairs and two ‘gooseberries’ the latter in several permutations. We should then expect the value to be some way below one third as the groups of three depreciate the figure from the sets of two and two. I was slightly surprised at how much more often the set of three conversations appeared than the two and two arrangement.
p(g6)=0.0998
Seven People [Yes, a heptagonal table!]
This was a good test of the logic built into the spreadsheet and the code. There can only be one value for p(g) each time as the guests can not be arranged other than three pairs and one ‘gooseberry’. Running simulations with seeds of 0.144 and 0.142 showed the value settle to one seventh to six decimal places within a little over a thousand steps.
p(g7)=0.142857
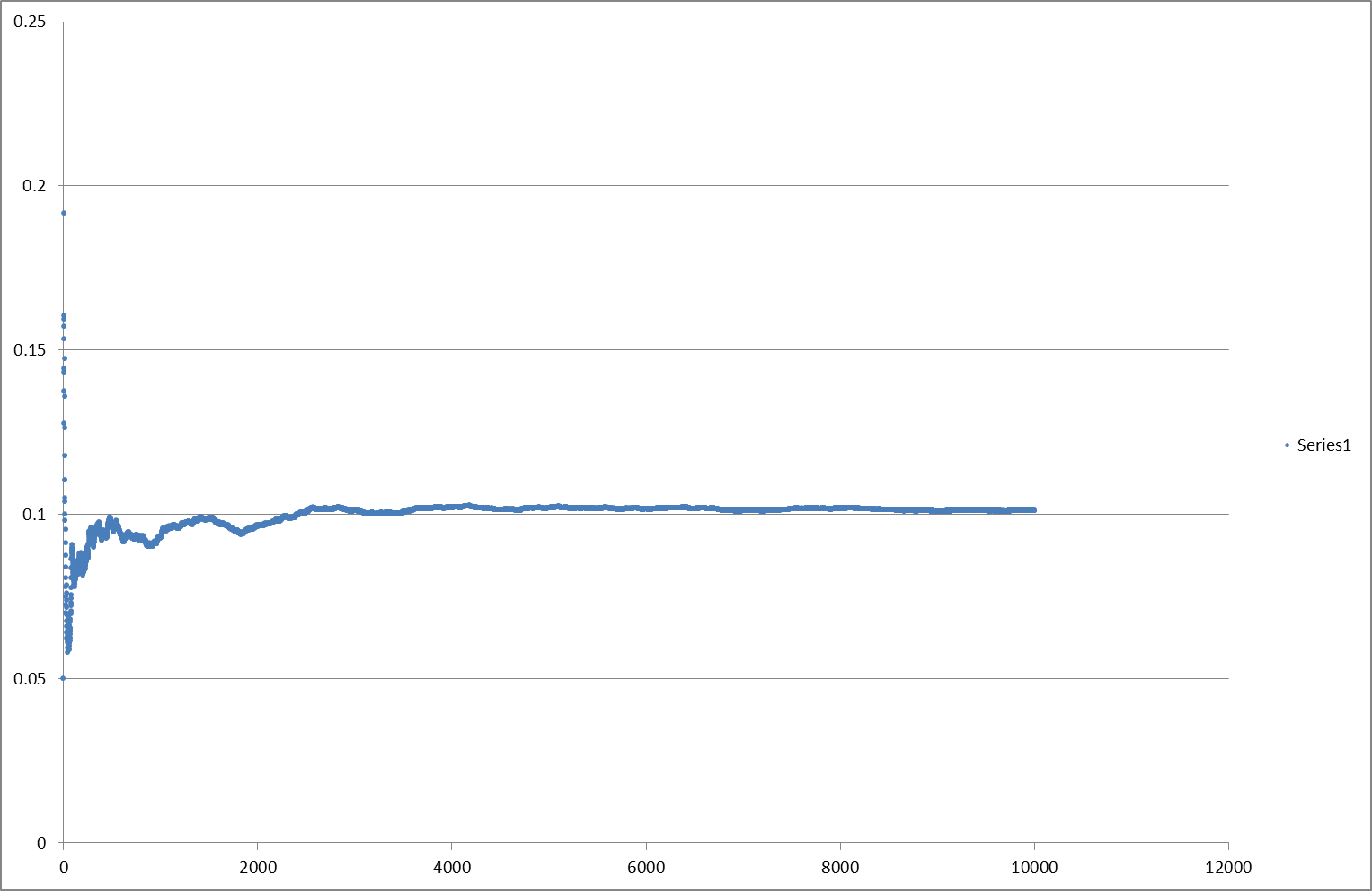
Eight People
Finally I felt ready to tackle the actual problem set! There are two possible stable configurations: four conversations or three pairs and two ‘gooseberries’ of which there are a number of permutations. We would thus expect a value some way below one quarter as the sets of four diminish the value from the sets of three and two, as with six guests.
p(g8)=0.1283
Even with a million loops the final value is only stable to three decimal places. However I am reasonably confident in the value expressed above. This has been an enjoyable challenge; I hope that I have shown that something as esoteric to most people as the Monte Carlo method can be applied to a simple model of a real life situation and be implemented in a straightforward manner with Excel, plus a touch of VBA.